11月30日の統計検定2級試験に向けて
統計検定2級の2013年、2012年、2年分の過去問を
2回目、勉強しました。

このままでは、少し理解不足だなぁとおもい、
Ｒと使って勉強を始めました。

あと、試験まで１５日強です。まだ現段階で
不安を感じていた、t検定、回帰分析までいたっていないので、
すこしあせりぎみ・・・

このＲをつかっての学習法は
実際に手を動かして計算するので、
面白いし、頭に入ってくるので、
がんばっております。

 

さぁ今日はこのＲによるやさしい統計学を勉強しはじめて、
ほぼ12日です。

Rによるやさしい統計学

本日は、その１０回目のレポートです。

今回は、

散布図を学びます。
散布図とは、２つの変数をプロットした図です。

①練習参加数をリフティング回数のﾃﾞｰﾀにつづいて入力してみましょう。

> 練習参加数<-c(30,40,50,55,40,60,30,40,50,55,40,60,40,50,55,40,60,30,40,50,55,40,60,30,40,50,55,40,60,40,50,55,40,60,100,80,70,100 + ) > 練習参加数
[1] 30 40 50 55 40 60 30 40 50 55 40 60 40 50 55 40 60 30
[19] 40 50 55 40 60 30 40 50 55 40 60 40 50 55 40 60 100 80
[37] 70 100
> リフティング回数と練習参加数の2変数の関係を図にしてみましょう。
> plot(リフティング回数,練習参加数)

お~プロットできました。
しかし、あまり関係性がなく、つまらないので、
ちょっと違ったデーターをもう一回入れてみたいと思います。

②リフティング練習週間に参加した回数との比較をしてみましょう。

> リフティング練習週間参加数<-c(30,48,42,60,70,46,50,45,70,80,45,58,45,70,80,56,55,45,60,70,40,60,80,50,60,50,60,80,50,50,50,70,80,40,50,40,70,80) > リフティング練習週間参加数
[1] 30 48 42 60 70 46 50 45 70 80 45 58 45 70
[15] 80 56 55 45 60 70 40 60 80 50 60 50 60 80
[29] 50 50 50 70 80 40 50 40 70 80
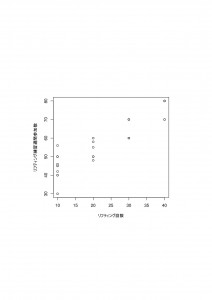
> plot(リフティング回数,リフティング練習週間参加数)

これはなんか相関がありそうな図となりました。

 

マンガでわかる統計学