統計検定2級の過去問を2年分
2回目の挑戦がおわりましたが、
t検定など理解不足を感じました。

過去問の繰り返し勉強は、
暗記していれば解ける問題には
即効性はあるのですが、
やはり、理解して解かないと
すこし問題をひねってだされると
回答が難しくなります。

 

 

ということで、
いまは、
このＲによるやさしい統計学を勉強しています。

Rによるやさしい統計学

本日は、その４回目のレポートです。

今回は、

質的変数

量的変数

という言葉を復習しました。

これも、統計検定では出てきたような言葉です。

質的変数は、男と女、数学が好きか、嫌いかなど、人を分けるのにつかう区分です。

量的変数は、具体的な数字が入ります。

数学の点数が100点、50点、33点、など、具体的な点数です。

質的変数のなかで、男と女などと、２つのうちから１つを選べるような場合は、
二値変数といいます。

この辺の用語は知っておきたいですね。

こんな言葉も、ただ教科書をよんでいると
頭に入らないのですが、
この参考書では、手を動かして実際にキーボードに入力を
していくと頭に入ります。

今回はまず、指導法A,B,Cの度数分布表を記載することを
覚えました。

> 指導法<-c(“A”,”B”,”B”,”C”,”B”,”A”,”C”,”B”,”B”,”C”,”B”,”A”,”C”,”B”) > 指導法
[1] “A” “B” “B” “C” “B” “A” “C” “B” “B” “C” “B” “A” “C” “B”
> table(指導法)
指導法
A B C
3 7 4

 

指導法A,B,Cを受けた人が、それぞれ3人、7人、4人です。

なるほど、なるほど。

リフティング回数<-c(10,20,10,30,40,10,20,10,30,40,10,20,10,30,40,10,20,10,30,40,10,30,40,10,20,10,30,40,10,20,10,30,40,10,20,10,30,40) > リフティング回数
[1] 10 20 10 30 40 10 20 10 30 40 10 20 10 30 40 10 20 10 30 40 10 30 40 10
[25] 20 10 30 40 10 20 10 30 40 10 20 10 30 40

 

リフティング回数というコマンドで、
リフティング回数を読み込むことに成功です。

これまた、面白いです。

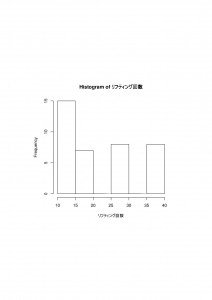
ヒストグラムも次のコマンドをつかって作成してみました。

 

> hist(リフティング回数

おお、なんか、役に立ちそうな気がしてきました。

リフティング回数をいれると、
よりそんな感じがします。

マンガでわかる統計学